- Original Paper
- Open access
- Published:
A demand model for international freight transport by road
European Transport Research Review volume 1, pages 23–33 (2009)
Abstract
This paper presents a system of models for the estimation of road international (import/export) freight flows by using a partial share approach. It allows to simulate generation (for export), attraction (for import) and distribution steps for the estimation of freight flows in quantities (commodity approach), from which the conversion in vehicles is made by using vehicle loading models. This modelling system has been specified according to an easy-to-use philosophy (suitable to be used for forecasting) by using aggregate variables, such as GDP. The calibration has been carried out by using a set of available data in Italy that allowed us to consider import/export flows by road for three different freight types (perishable, industrial and consumption goods).
1 Introduction
The increasing of the world merchandise trade reached the 8% in 2006, while the increasing of world gross domestic product (GDP) in the same period has been estimated at 3.5% [26]. Analysing the time series of these two indicators in the period 2000–2006, it is possible to point out that the growing trend of world merchandise trade is about twice the annual growth rate.
European statistics by road [10] show that road freight flows are the main reason of congestion. Stakeholders have to be supported with adequate models and tools in order to forecast the demand and to assess the network performance that reflects on shipping efficiency. This is a crucial point if, besides to transportation issues, we also consider the opportunities provided by logistic services like groupage/degroupage (i.e. components manufactured in different locations must be transported to a single location for assembly before being shipped abroad again).
Freight transportation is usually measured and described by either commodity or vehicle movements. Freight demand is derived from the socioeconomic system in which raw materials, intermediate inputs and finished products are needed at specific locations in precise times. Therefore, the primary focus on freight transportation demand modelling should be on commodity movements since vehicle movements are triggered by the need to move commodity.
At international level, the aim of this class of models is to estimate goods movement between different countries. International goods movement has had explosive growth in the last decade due to the East locations of operations of multinational firms as a way to take advantage of competitive prices for both materials and labor.
Demand models play a key role for transportation planning. Public agencies need to forecast future transport requirements for both people and commodities in order to provide infrastructures and services that make possible such movements. The private sector needs to forecast demand for transportation services to anticipate, among others, future financial requirements, equipment acquisition and labour requirements.
Models developed to simulate the international freight flows can be classified as aggregate or disaggregate according to used variables. Aggregate variables concern, for example, data of all companies of a certain category and/or economic sector; disaggregate variables concern, for example, data on individual companies or individual shipments. Moreover, a further classification can be done according to model structure in partial share models (multi-step models) and joint/direct models. Partial share models consider a progressive split of the whole process into different steps (e.g., generation, distribution and modal split) within which every sub-model of the sequence is treated/solved independently of the others. Joint/direct models differ from the previous ones because the whole process is simultaneously approached (all in one).
In the literature, international freight flows have been investigated by many authors through the use of systems of models that can be difficult to calibrate and apply (see Section 2). In order to estimate a first magnitude of import/export freight transport by road, this paper proposes an aggregate modelling system specified by using a partial share approach. The modelling system has been specified by aggregate variables and has been calibrated by means of data collected in Italy, including data gathered through road surveys. In the following, Section 2 presents the state-of-the-art of models for estimating the international freight transportation; Section 3 introduces the structure of the proposed modelling system, and Section 4 describes calibration results, while Section 5 reports the conclusions of this work.
2 State-of-the-art
An exhaustive review of models which simulate international freight transportation is given by Regan and Garrido [18]. Most of them analyze the international freight transport referring to shipping. According to Haralambides and Veenstra [12], three main modelling approaches can be identified.
The first approach follows the standard theory of international trade [14], which allows the indirect inclusion of transportation costs; the standard trade theory is concerned with the pattern of trade between two or more countries, based on the Ricardian principle of competitive advantage.
The second approach is based on an aggregate cost function for a given industrial sector, from which a demand function is derived [17].
The third approach is the use of spatial interaction models to estimate trade flows, for which the most widely used model is the gravity one [13, 15, 25] generally used to estimate bilateral trade flows [2]. The main advantage of these models, which makes them attractive for applications, resides in modeling flows rather than freight demand. However, as they are cross-section models they are not adequate for forecasting purposes, like demonstrated by Regan and Garrido [18].
In literature, very few works have been developed for freight transportation at international level; most of them are simple models that neglect modal split and path choices and are used to support the estimation of freight transportation quantities. Coto-Millàn et al. [8], for example, present a theoretical explicative model and provide empirical evidence to the determinant variables, which explain the behaviour of maritime imports and exports for a particular case (the Spanish economy). The complexity resides in the specification of a coherent and coordinated system of models, that includes the well-know sequence of generation, distribution, modal split and path choice, to which the departure time and terminal choices have to be added to simulate some of the crucial patterns of international freight transport. Dependences and feedbacks of this problem do not allow to use alternative approaches; for example, the use of time series that leads the relevant approximations when unexpected “breaking” phenomena occur (e.g. a particular and unexpected event in the global economy).
A direct relation between international freight movements and transportation costs is given in Bougheas et al. [3]. This model is a useful tool for estimating benefits from the current stock of infrastructures of the home and foreign countries. The transportation cost function does not only depend on traveled distance but also on freight volume, network structure and competing transportation services for a given O/D pair. Some researchers add dummy variables to this model in order to incorporate the spatial effect of a common border as well as of a common language. The consideration of the common border is a key variable in the process of trade between two countries needs to be explored in more detail as an enormous variety of specifications can be applied to address the same spatial issue (see for example Anselin [1]).
A similar problem was addressed by Garrido [11] in an analysis of truck flows through the Texas–Mexico border. This model addresses the trade in terms of truck flows instead of commodity flows, and incorporates directly the spatial connectivity (instead of including a dummy variable for this purpose). The model showed the significant correlation between the freight movement in different bridges along the border. The model was used to evaluate the impact on the service performance at the border crossings due to marginal infrastructure improvements.
The well-known family of models based on input–output analysis has also been used for modeling freight transportation demand, both at intercity and international level. A number of operational land use-transportation models make use of spatial input–output (SIO) models, some of which are based on random-utility theory. The random-utility-based multiregional input–output (RUBMRIO) model has been solved in practice by iteratively applying a set of equations. Zhao and Kockelman [27] examine the existence and uniqueness of the RUBMRIO solution, which represents the spatial allocation of productive activities and commodity flows.
Finally, an example of application to a wide area (Mediterranean zone) was developed by Russo and Assumma [20]. They propose a system of models in order to reproduce the current situation in the Mediterranean basin by using a statistical-descriptive approach. Generation, distribution and mode-service choice models have been specified and calibrated for the study area.
Latest experiences in this field point out that most recent and sophisticated systems of models for freight demand estimation have been carried out by the integration of two classes of models: macroeconomic models, which simulate the level (quantity) and spatial distribution of goods exchanged between different economic zones (leading to origin–destination matrices), and behavioral models that simulate mode and route choice. Considering the described complexity, this paper proposes a system of models that aims at reducing the complexity of the macroeconomic models and allows for obtaining a first estimation of import and export by road, both in terms of quantity and vehicles. Such a system of models could be used, for example, in the context of studying the effects of future strategies on freight transport.
3 The proposed modelling system
In the sphere of demand model classification of Section 2, the proposed modelling system can be classified as a partial share one. It characterizes import/export freight flows by road as:
-
origin and destination (respectively o and d);
-
time period (h);
-
freight type (s), e.g. perishable goods, non-perishable, and so on;
-
average delivered/picked freight quantity (q);
-
vehicle type (v).
The proposed system of models allows to simulate the average flow of goods (Q) and vehicles (VC) by road using generation (for export flows), attraction (for import flows), distribution and vehicle loading models. These models allow us to carry out freight flows both in quantities and vehicles by considering (Fig. 1):
-
a commodity level, in which the freight O/D matrices in quantity are estimated from socioeconomic data;
-
a vehicle level, in which quantity flows are converted in order to obtain O/D matrices in vehicles (e.g. trucks or lorries).
The following subsections specify each of the models belonging to the proposed system of Fig. 1.
3.1 Attraction and generation models
Attraction and generation models are specified within the commodity level; they allow us to estimate the freight attracted (import) and generated (export) by each traffic zone from (import) and to (export) foreign countries.
For what concerns the attraction model, the average flow of freight quantity of type s attracted by zone d in time period h (e.g. year or day),  , can be estimated by a descriptive model belonging to the category regression class, for which
, can be estimated by a descriptive model belonging to the category regression class, for which  can be expressed as a function, typically linear, of variables
can be expressed as a function, typically linear, of variables  representative of freight type s and destination zone d, as:
representative of freight type s and destination zone d, as:

where  are the model coefficients to be estimated and
are the model coefficients to be estimated and  is the error component.
is the error component.
In order to estimate the export, the generation model allows us to estimate the average flow of freight type s departing by road from zone o in time period h,  , that can be expressed by a category regressive model, specified through variables representative of freight type s and origin zone o, as:
, that can be expressed by a category regressive model, specified through variables representative of freight type s and origin zone o, as:

where  are the model coefficients to be estimated and
are the model coefficients to be estimated and  is the error component.
is the error component.
Attributes Xs of Eqs. (1) and (2) represent socioeconomic variables (such as income or GDP) and level of service ones (such as zone accessibility or transportation costs).
3.2 Distribution models
Distribution models are used to obtain the spatial share; they can be differently specified for import and export freight flows.
Distribution models can be interpreted and specified following either a behavioural or a descriptive approach with various specifications and interpretations of the attributes [4]. According to the behavioural interpretation, the distribution model simulates the choice of a destination among possible alternatives. It should be noted that typically the chosen alternative for carrying out an activity is not a traffic zone but one (or more) elementary alternatives (such as a firm, a general market, etc.) located within the zone. The traffic zone is therefore a compound alternative made of aggregation of elementary alternatives.
Variables considered into the distribution model can be divided into two groups: variables representing the activity system, which measure the generation/emission or attraction power of a given zone for freight type s (e.g. wholesale employees of freight type s), and variables representing cost or separation attributes, which measure the generalized travel cost for transporting goods of type s on the od pair.
Referring to import, the distribution model allows us to obtain from which zone o the freight arrives to zone d (destination constrained); in other words, it gives the probability p[o/dsh] that freight attracted by zone d arrives from zone o. Referring to a multinomial logit structure, this probability can be expressed as:

where
- V o :
-
is the systematic utility of zone o, that can be expressed as a linear combination of attributes;
- I d :
-
is the set of possible origin zones within the study area from which freight can arrive to zone d;
- θ o :
-
is the parameter of the Gumbel random variable.
For export, the distribution model (origin constrained) allows us to carry out the probability p[d/osh] that freight generated from zone o is destined to zone d. As described for import, referring to a multinomial logit structure, this probability can be expressed as:

where I o is the set of possible destination zones for freight departing from zone o.
Besides the specification of behavioural models, in many real applications descriptive distribution models are used. One of the models that allows to reduce this complexity and to eliminate the influence of the level of spatial disaggregation adopted is the simply constrained gravitational model. For example, in the case of import, the probability p[o/dsh] can be expressed by activity system ( ) and cost of separation (C
od
) variables, as:
) and cost of separation (C
od
) variables, as:

where  are the model coefficients to be estimated.
are the model coefficients to be estimated.
The probability p[d/osh] for the export can be expressed in the same way.
Finally, the average flow of freight type s between zones o and d in time period h can be obtained as follows:

where
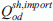 and
and  :
:-
are the average import and export flows of freight type s between zone o and d in time period h;
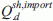 and
and  :
:-
are the average import and export flows estimated, respectively, by Eqs. (1) and (2);
- p[o/dsh] and p[d/osh]:
3.3 Vehicle loading models
Freight transport is strictly related to the logistic system considering all operations from supplying to final distribution that allows freight to arrive from supplier to producer and, then, to consumer. In general, the logistic systems are composed by several Logistic Center (LC), where some activities (e.g. groupage/degroupage, assembly, packing, storage, etc.) are carried out.
This aspect reflects on vehicle type choice because choices of transport modes and transportation management are different if we consider the problem of feeding producers (both raw materials and intermediate products) from suppliers (supplying process), or if we consider the freight transport to the final distribution (distribution process). The distribution process can be deepened on Nuzzolo et al. [16], while the supplying process is here shortly recalled aiming at defining the freight quantity–vehicle conversion.
The use of a particular supplying channel defines the average size of shipment and hence the type of vehicles to be used. In other words, the direct shipping of freight from the supplier to the producer implies an average shipping size of goods higher than that shipped to a logistic center; this influences the type of vehicle to be used (in terms of capacity), and hence the estimation of the number of vehicles moving on the road network. This is a crucial point, for example, in capacity analysis studies.
From data described in depth in the following section (Section 4) it was revealed that less than 3% of freight moved between supplier and producer by road at international scale passes through a logistic center. For this reason, in order to reduce the complexity of the proposed modelling system, the supplying model will be neglected.
Given commodity flows, it is possible to estimate road freight flows in vehicles by using a vehicle loading model. Even if this kind of models play a crucial role in the commodity-based modelling framework, few works in the literature refer to this aspect (usually for the estimation of the distribution stage) by considering the quantity–vehicle transformation through approximation fixed rates that are useful for capacity analysis studies.
Vehicle loading models should consider:
-
the capacity and the average transportable quantity by each type of vehicle;
-
the nature of the consignment; the proportion of vehicle capacity required by each consignment and the aggregate volume of consignments by each shipper in a specific time period;
-
the characteristics of the desired pick up and delivery vehicle patterns.
Given the O/D matrices in quantity, through Eq. (6), the number of vehicles that are necessary to transport the quantity  by vehicle type v is given by:
by vehicle type v is given by:

where
-
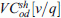 :
: -
is the number of vehicles of type v moving freight type s on the O/D pair od in time period h, which refers to average transported quantity
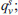
-
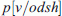 :
: -
is the vehicle type share obtained by a vehicle type model, which represents the share of vehicle type v used to move freight on the O/D pair od.
In general, Eq. (7) can be specified both for import and export. In fact, depending on the characteristics of freight demand it is possible to have different vehicle type models and then different average transported quantities by each type of vehicle. The vehicle type model can be also specified in the framework of the RUM (random utility model) theory by using (for example) a multinomial logit model.
4 Specification and calibration
The system of models described in the previous section has been specified and calibrated for Italian import/export flows by road. Three main data sources have been used:
-
Italian census data, where the socioeconomic information is aggregated per economic sectors under ATECO classification used by ISTAT (Italian National Institute of Statistics), which derives from the international NACE classification;
-
Eurostat data, in order to characterise analysed import/export flows for the Italian border countries;
-
Surveys to truck drivers carried out in Italian Alps Cross Borders.
The study area (Europe) has been divided into traffic zones by considering different levels of detail. Italy has been divided into 103 traffic zones at province level because the models have been specified for Italian import/export. For this reason, the zoning for Italy is more detailed than rest of Europe. The zoning of the other European countries has been carried out by the European Nomenclature of Territorial Units for Statistics (NUTS) at level 1.
According to other Italian studies developed in this field [19], the used freight classification consists of aggregation of NST/R (Goods Nomenclature for Transport Statistics/Revised–Eurostat) in freight types as:
-
perishable goods, given by the aggregation of class 0 and 1;
-
industrial goods, given by the aggregation of class 2, 3, 4, 6, 7 and 8;
-
consumption goods, given by the aggregation of class 5 and 9.
Referring to year 2005, Table 1 reports the import/export freight type distribution according to this classification. Percentages of Table 1 refer to a total amount of 43 million of tons (corresponding to 40,245 million of tons-kilometres) that have been moved by road. The 48% of the whole amount refers to the import, for which the 57% is destined to the Northern Italy and only the 17% to the Southern Italy. For what concerns the exports flows, about the 65% of freight has origin in the North and about the 16% in the South of Italy. Referring to the freight type, about the 55% of imported freight belongs to consumption goods.
Analysing available data of the last 10 years (1998–2007), it is possible to point out an increase of 88% and 41% for import and export, respectively. Moreover, about the 4% of international freight transport quantities are moved by road in own account with an average trip-distance of about 360 km against the 850 km travelled by third parties [6].
In order to characterize and investigate the import/export freight flows in Italy some surveys have been carried out. Surveys allowed us to have some information on the current and reverse journey in terms of origin and destination, characteristics of transported freight (e.g. type, quantity and so on), used vehicles (e.g. model, swept volume, tow presence, and so on), number of drivers, driver characteristics (e.g. age, sex, and so on) and some route characteristics such as the use of highways or otherwise. Survey data used for calibration consists of about 2000 interviews. Models have been calibrated using the generalized least squares (GLS) estimator within the classic theory of statistical inference. The presented models are the result of several specifications and calibrations based on different combinations of possible attributes. In the following models that performed the best statistical significances are reported.
4.1 Attraction and generation models
Referring to the structure of the system of models proposed in Section 3, aggregate attraction and generation models of the index per category class have been specified and calibrated. The average quantity of freight of type s attracted by zone d (for the import) or generated by zone o (for the export) in time period h (e.g. a day) can be expressed as a function of the:
-
total number of inhabitants and employees in zone z, ER z ;
-
number of employees of zone z referred to freight type s,
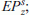 ;
; -
average per-capita income in zone z, IC z ;
-
average per-capita gross domestic product in zone z, GDP z ;
-
dummy variable NT z , that is equal to 1 if zone z is located in the North of Italy (i.e. near the border among Italy and other European countries), 0 otherwise;
-
dummy variable PT z , that is equal to 1 if there is a port within zone z, 0 otherwise;
The proposed attraction model allows us to estimate the import flows by road as a function in the coefficients  of the above described attributes (or by some functional transformations of them such as the natural logarithm) as follows:
of the above described attributes (or by some functional transformations of them such as the natural logarithm) as follows:

Table 2 reports values of  parameters calibrated for the three freight types of Table 1. All parameters are correct in sign and are statistically significant as shown by t-student values. The capability of models to reproduce the revealed values is shown by values of ρ2 similar to those present in the literature.
parameters calibrated for the three freight types of Table 1. All parameters are correct in sign and are statistically significant as shown by t-student values. The capability of models to reproduce the revealed values is shown by values of ρ2 similar to those present in the literature.
Results highlight that for all type of freight the presence of a port within the traffic zone, which reduces the road use, is relevant (especially for long trips). This variable for consumption goods is greater than other types of freight. Deepening on the analysis of consumption goods, the attraction is measured by the number of inhabitants and the number of employees while for the other freight types the attraction power is explained by the number of employees, only. Moreover, for perishable and consumption goods the income is relevant, while it is replaced by GDP for industrial goods as this freight type represents the most part of the economy of a country whose levels of productivity are better measured by GDP.
As described for the attraction model, the proposed generation model allows us to estimate the export flows by road as a function in the coefficients  of the above described attributes as follows:
of the above described attributes as follows:

Table 3 reports values of  parameters calibrated for the three freight types of Table 1. All parameters are correct in sign and are statistically significant as shown by t-student values, as well as values of ρ2 are similar to those present in literature for models of this type.
parameters calibrated for the three freight types of Table 1. All parameters are correct in sign and are statistically significant as shown by t-student values, as well as values of ρ2 are similar to those present in literature for models of this type.
In the case of export, the emission power is measured with the number of employees, and the parameter for perishable goods is about twice than that calibrated for consumption goods. In the estimation of the generation for industrial goods the weight given by the GDP is more relevant, with a similar effect of that described for the attraction model.
It is interesting to compare calibrated parameters for import and export. At first, we can see that the attraction and emission power of each zone is measured by the number of employees. In the case of import of perishable goods, the presence of pro-capita income and variable NT, that characterizes border zones, is important. In the case of industrial goods, the difference between import and export functions is given by the presence of an available port (variable PT) for the import; the negative value of β PT demonstrates that the presence of a port in a province drives freight flows to the competition with maritime transport, which reduces the road use. There is also a substantial difference between import and export functions for consumption goods: the number of inhabitants representative of import is replaced by the number of employees for the export.
Referring to the two dummy variables (NT and PT), it is possible to note that the variable NT is statistically significant only for perishable goods in the case of import and for industrial and consumption freight classes in the case of export. For what concerns the variable port (PT), it is statistically significant for all freight in import and, only for perishable goods in the export case.
Even if the presented models allow us to estimate generation and attraction using basic socioeconomic and land-use attributes, at the initial stage of some studies, the analyst is sometimes required to provide a first estimation of future import/export flows by using available data from other studies (e.g. territorial ones), that typically report population and employees forecasts [24]. For this reason, simplified models for  and
and  , based only on the number of employees
, based only on the number of employees  of the generic zone z, have been specified and calibrated as follows:
of the generic zone z, have been specified and calibrated as follows:

where  is the model parameter, whose calibration is reported in Table 4.
is the model parameter, whose calibration is reported in Table 4.
Calibration results of Table 4 point out that the value of ρ2 is lower than that reported in Tables 2 and 3. It confirms the need of using other explanatory variables for both freight flows (import and export) and freight types, as successfully done in the specification of such models reported in Eqs. (8) and (9); it also points out the limit of models described by Eq. (10) that are suitable to be used for an approximated initial estimation of distribution and attraction when a very limited number of data are available.
4.2 Distribution models
In order to know the origin of freight for a given attraction zone d (for import) and the destination of freight for a given generation zone o (for export), some descriptive distribution models have been specified and calibrated. The distribution model for the analysis of import flows is constrained to the destination. The probability p[o/dsh] that freight type s attracted by zone d in time period h arrives from zone o can be written as:

where
-
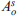 :
: -
is the number of employees of zone d referred to freight type s;
- C od :
-
is the average travel generalized cost by truck between zone o and d.
-
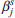 :
: -
are model coefficients to be estimated.
For what concerns the analysis of export flows, the distribution model is constrained to the origin; it has been specified and calibrated for giving the probability p[d/osh] that freight of type s generated by zone o in time period h is destined to zone d as:

where the variables have the above described meaning.
Level-of-service attributes composing the generalised cost C od have been calculated by using a road network model. It is made of the primary road network (motorways, state roads and so on) of the whole Europe. The average path cost for a generic od pair, C od , can be calculated as:

where
-
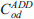 :
: -
is the additive path cost, defined as the sum of the link-wise additive link costs,
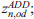 ;
; -
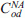 :
: -
is the non-additive path cost.
The additive cost is a combination of attributes among which travel time and travel monetary cost are the most important. Referring to travel time, it was calculated as the sum of the on-road travel time and stop time.
The on-road travel time has been calculated as the sum of travel time on freeways, extra-urban roads and other types of roads. Travel time for each type of road has been estimated using the link-cost function proposed by CNR [5] and TRRL [21–23], which has been properly updated for the study case [7].
Stop time derives from the EU Regulation [9] that sets two constraints:
-
breaks (after four-and-a-half hours’ driving, the driver shall observe a break of at least 45 min, unless he begins a rest period),
-
rest periods (in each period of 24 h, the driver shall have a daily rest period of at least 11 consecutive hours).
Even if distribution models have been calibrated both for import and export flows, similar results have been obtained. For this reason, Table 5 reports a unique set of parameters to be used for both import and export. By analyzing results of Table 5 it is possible to point out that the number of employees plays in the same way, while the weight is more than twice for consumption goods. The ρ2 values over 0.80 show the goodness of the models to reproduce the revealed spatial share.
4.3 Vehicle loading models
Given the O/D matrices in quantity, these matrices have to be converted into vehicles by Eq. (7).
The vehicle type share p[v/modsh] has been estimated by collected data. The surveys carried out to truck drivers at the Italian Alps cross Borders, previously described, allowed us to identify origin and destination of journey, as well as used type of both freight and vehicle. Through the road vehicle classification used by Eurostat [10], it is possible to analyse the results of these surveys in terms of distribution per vehicle type and average load. Table 6 reports the estimated vehicle type shares and the relative average transported quantities  for the following vehicle types v:
for the following vehicle types v:
-
Goods vehicles with transportable quantity less than 18 tons,
-
goods vehicles with transportable quantity more than 18 tons, divided in:
-
articulated lorry,
-
lorry with trailer.
-
Analysing data of Table 6, about the 76% of international transport pertains to trucks with capacity higher than 18 tons, which move an average load of about 14 tons per vehicle (load factor near 80%). Lorries with trailers represent about the 10% of the whole but their average transported quantity is about 22% more (16.7 tons) than that of articulated lorries. Goods vehicles with transportable quantity less than 18 tons represent about the 14% of trucks; they move about 10 tons per vehicle and hence, considering the average ratio with vehicle capacity, they have the highest load factors.
The following Tables 7, 8, 9, 10 show vehicle shares per length of journey (class of distance). According to EU Regulation [9], three classes have been identified:
-
driving time less than 10 h (about 800 km) corresponding to a journey with one driver and without rest period;
-
driving time between 10 and 19 h (less than 1,500 km) corresponding to a journey with two driving cycles;
-
driving time more than 19 h.
From the aggregate analysis (Table 7) emerges that the average vehicle share decreases with increasing of driving time for heavy goods vehicles (goods vehicles >18 tons). For the other classes of vehicles we have the opposite.
If the analysis is carried out for freight type (Tables 8, 9, 10), we find a similar trend for perishable goods where the average shares to use an articulated lorry are less than 83%. For industrial and consumption goods these shares are less than 75%.
For industrial goods (Table 9) we can see that the share of using vehicles with less than 18-tons capacity is the minimum for the medium class of distance. This effect is the opposite analysing consumption goods where it corresponds the maximum use of this vehicle type (Table 10).
5 Conclusions
This paper presented a modelling system for the estimation of international (import/export) freight flows by road. It uses a partial share approach to simulate the generation, attraction and distribution steps for the estimation of freight flows in quantities (commodity approach), from which the conversion in vehicles is made by using vehicle loading model.
The modelling system has been specified through easy-to-capture variables (especially for its forecasting use) represented by level-of-service attributes and aggregate socioeconomic variables, such as GDP and employee number.
Besides the specification of the modelling system, the calibration to the Italian case study on the basis of the latest panel of available data allowed us to set up an easy-to-apply system of models. It can be used for an initial estimation of the generation and attraction potentials of import/export for a given zone by considering different freight types (perishable, industrial and consumption goods).
Regarding the calibration, results show that all obtained parameters are statistically significant both in expected sign and validation statistics. From the analysis of import it emerged that the per capita income is relevant for perishable and consumption goods, at same way of the gross domestic product for industrial goods both for import and export, even if the influence on export is about double respect the import flows. Furthermore the presence of a port inside the zone determines a reduction of road flows due to the attractiveness of maritime transport, especially for long trips.
This system of models can be successfully used for the estimation of import/export freight flows by road in the initial assessment of future scenarios, as well as to calculate the import/export potentialities of a given zone such as the generic Italian province of the calibration phase.
Further developments of this research mainly regard two main topics: the possibility to extend the proposed modelling system to the supplying choice dimension, the vehicle type model and the possibility to develop a complete modelling system according to the four step model. The supplying choice model could be an useful tool for investigating how the choice of using or not a Logistics Center can influence the used vehicle. In fact, the use of a particular supplying channel could influence the average size of shipment and hence the type of vehicles to be used. Referring to vehicle type model, in the literature some models were developed for simulating the choice of private cars, but there are few models for the simulation of truck holding choice. This model could be specified and calibrated according to RUM theory where the systematic utility could be considered as a function of some attributes related to firm dimension (e.g. employees), shipment (e.g. frequency, length of journey) and vehicle features (e.g. payload). Other developments could aim to develop a complete modelling system that considers all transport mode for import and export by introducing a model to simulate the modal split. In this case, the estimation of an OD matrices requires the implementation of a more sophisticated distribution model, which should also include a balance procedure that considers the equilibrium between row and column sums. In other words, the estimation of the average import/export flows should be checked to be double constrained estimations since the imports of a zone (presented as origin from a specific destination) must be equal to the export of the specific destination to the presented origin.
References
Anselin L (1988) Spatial econometrics: methods and models. Kluwer, Boston, USA
Black WR (1972) Interregional commodity flows: some experiments with the gravity model. J Reg Sci 12:107–118
Bougheas S, Demetriades P, Morgenroth EL (1999) Infrastructure, transport costs and trade. J Int Econ 47:169–189
Cascetta E (2001) Transportation systems engineering: theory and methods. Kluwer, The Netherlands
CNR (1980) Norme sulle caratteristiche geometriche delle strade. Roma
CNT (2007) Conto Nazionale delle Infrastrutture e dei Trasporti (CNIT)–Anno 2005–con elementi informativi per l’anno 2006. Ministero dei Trasporti, Rome, Italy
Comi A, Russo F, Vitetta A (2005) Calibration of generalized cost models for road freight vehicles within an intermodal chain: an experimental application in Italy. Proceedings of European Transport Conference, Strasbourg, France
Coto-Millàn P, Banos-Pino J, Villaverde Castro J (2005) Determinants of the demand for maritime imports and exports. Transp Res Part E 41:357–372
EEC (3820/85) Harmonisation of certain social legislation relating to road transport. Official Journal of the European Communities, Bruxelles
EuroStat (2008) Road freight transport by type of goods—2006. European Commission, Bruxelles
Garrido RA (2000) Spatial interaction between the truck flows through the Mexico–Texas border. Transp Res Part A 34(1):23–33
Haralambides H, Veenstra A (1998) Multivariate autoregressive models in commodity trades. Proceedings of 8th World Conference on Transport Research Conference, Antwerp, Belgium
Hartwick JM (1972) The gravity hypothesis and transportation cost minimization. Reg Sci Urban Econ 2:297–308
Mundell RA (1957) Transport costs in international trade theory. Can J Econ Polit Sci 23(3):331–348
Nijkamp P (1975) Reflections on gravity and entropy models. Reg Sci Urban Econ 5:203–225
Nuzzolo A, Crisalli U, Comi A (2008) Metropolitan freight distribution by railways. In: Taniguchi E, Thompson RG (eds) Innovations in city logistics. Nova Science, Hauppauge NY, USA
Oum TH, Waters WG II, Yong JS (1990) A survey of recent estimates of price elasticities of demand for transport. Policy Planning and Research Working Papers, WPS 359
Regan AC, Garrido PA (2000) Modeling freight demand and shipper behaviour: state of the art, future directions. Preprint IATBR, Sydney, Australia
Russo F (2005) Sistemi di trasporto merci—approcci quantitativi per il supporto alle decisioni di pianificazione strategica tattica ed operativa a scala nazionale. Franco Angeli, Milan, Italy
Russo F, Assumma V (2007) An aggregated system of transport models for the Mediterranean free trade zone. Proceedings of 11th World Conference on Transport Research Conference, Berkeley, USA
TRRL (1980a) A study of speed/flow/geometry relations on rural single carriageways. LF 923
TRRL (1980b) Speed/flow/geometry formulae for rural single carriageways. LF 924
TRRL (1980c) Changes in speeds on rural roads. LF 925
Wagner T (2008) Planning for logistics and distribution facilities in the Hamburg region. Proceedings of European Transport Conference, Noordwiikerhout, The Netherlands
Wilson AG (1974) Urban and regional models in geography and planning. Wiley, London
WTO (2007) International Trade Statistics 2007. World Trade Organization, Switzerland
Zhao Y, Kockelman KM (2004) The random-utility-based multiregional input-output model: solution existence and uniqueness. Transportation Research Part B 38, Elsevier
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License ( https://creativecommons.org/licenses/by/2.0 ), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Nuzzolo, A., Crisalli, U. & Comi, A. A demand model for international freight transport by road. Eur. Transp. Res. Rev. 1, 23–33 (2009). https://doi.org/10.1007/s12544-008-0003-0
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s12544-008-0003-0

 and
and  :
: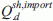 and
and  :
: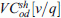 :
: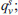
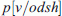 :
: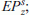 ;
;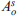 :
: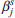 :
: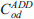 :
: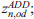 ;
;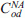 :
: