- Original Paper
- Open access
- Published:
An analysis of the determinants of local public transport demand focusing the effects of income changes
European Transport Research Review volume 5, pages 101–107 (2013)
Abstract
Purpose
In order for public transport to be a part of the solution to the environmental problems caused by traffic there need to be a clear understanding of how, and to what extent, different factors affect demand. There still seem to be some confusion regarding some key relationships, one of them being the effect of income on public transport demand. The purpose of this article is therefore to provide empirical estimates of how different factors, including price and car ownership (although income being the main issue), affect the demand for local public transport.
Methods
In order to achieve the aim of the study, an econometric FD-model, allowing for unobserved effects, was estimated using panel data from Swedish counes from 1986 to 2001.
Results
The short-run (direct) elascies with respect to fare, vehicle-kilometres, income and car ownership were found to be −0,4, 0,55, 0,34, and −1,37 respectively. However, income affects public transport demand directly, and through its effect on car ownership, these effects works in opposite direction. Combining these it is found that total income effect is close to zero.
Conclusions
It is concluded that, although the findings of several previous studies suggests that demand for public transport might be falling with increased income, there is no evidence of such effects even when the full effect of changes in income (including changes in car ownership) is taken into account.
1 Problem and purpose
For a long time increasing car and truck traffic volumes have gone hand in hand with increasing economic activity. This development has led to increased traffic congestion as well as to wider environmental problems, and threatens to further do so. Despite this, private car continues to gain market shares at the expense of public transport in most urban areas of the industrialised world. In order to explain this development, and provide a basis for policy, a large amount of studies have been performed and published [1–4] provide overviews of previous results.
In view of all the previous research in this area it is strange that it has not been used in order to reverse the negative development. There are several (non-excluding) possible explanations of this. One is that the political commitment to promoting public transport is not strong enough when it comes to actually providing the necessary resources. Another possible explanation is that, although well meaning, the decision makers is forced by the harsh reality of Baumol’s cost disease to continuously increase fares and reduce quality of service in order to keep the level of subsidies from increasing. A third explanation might be the uncertainty that seems to be present as regards key relationships affecting public transport. In a meta-analysis Holmgren [5] shows that estimated fare elasticities range from zero to −1,32, and demand elasticities with respect to service level range from almost zero up to 1,9. The most striking variation concerns the effects of income on public transport demand. In this case the estimations range from almost minus one (−0,82) up to well above one (1,18). In other words, there is no consensus even as to the sign of the income effect. Results exhibiting this kind of variation make a poor base for policy recommendation. If the income effect is in fact negative, it would be difficult for public transport to act as part of a long-run solution to the environmental problems caused by the transport sector.
The main focus of most previous studies has been the effect of fares and the effect of quality of service (usually measured by vehicle-kilometres) [5]. This is understandable since these variables are considered to be under direct control of the supplier of public transport, but in order to understand the past development and predict the future, other variables must also be considered.
Nijkamp and Pepping [6], Kremers et al. [7], Holmgren [5], and Hensher [8] have used meta-analysis in order to explain the variation in previous results and conclude that the specification of the model greatly affects the results but also that some of the variation is due to regional differences, the time period observed, and the type of data used. Based on these studies, two important questions which need to be examined further can be identified due to the lack of previous information or the presence of a large degree of uncertainty. Those are the interrelationship between demand for public transport and quality of service and the question of the total income effect.
Public transport patronage is generally found to be highly correlated with quality of service, vehicle-kilometres or vehicle-kilometres per km2, and the latter is often used as an explanatory variable in demand functions. The problem is that there are good reasons to believe that although quality of service certainly affects demand, the level of demand also affects the level of service. This issue has been raised by several authors, the perhaps most influential being Mohring [9–11] who showed that capacity and quality of service were joint products. His models have also been extended and generalized by Jansson [12, 13] and by Jara-Diaz and Gschwender [14] (see also [15–20] for cases were this has been mentioned but incorporated into the model) Despite this, the most common practice in statistical/econometric applications is to assume that quality cause demand and not the other way around. Holmgren [21] applied a Granger causality test to Swedish data and concluded that there was a two-way relationship between public transport patronage and vehicle-kilometres. Failing to take into account a prevailing two-way relationship when estimating a demand model will result in biased estimates.
Previous, empirical, studies where level of service has been treated as an endogenous variable, has been based on different assumptions as to the behaviour of the public transport supplier. These include supply functions derived from assuming profit maximisation, passenger maximisation and maximisation of operations as well as various ad hoc formulations of supply functions. Although useful contributions to the knowledge of public transport have been made through such assumptions, which might accurately capture producer behaviour in some cases, they fail to point out the key element of supply and demand interaction in the case of public transport: the fact that capacity and quality are joint products. Increasing (decreasing) capacity will also increase (decrease) the quality of service. This is most obvious when capacity is expanded by increasing the number of vehicles in use. In that case waiting times are reduced by shorter headway [9–11].
The purpose of this article is to investigate the effects of income changes on local public transport demand. In order to do this, a demand model, taking into account the two-way relationship caused by the jointness of capacity and quality is estimated. Increased understanding of the long-run effects of income changes on public transport demand will improve the possibilities of making accurate forecasts and efficient planning.
2 The Swedish data
The study uses annual data of the urban traffic of the 26 Swedish counties from the period of 1986 to 2001. Due to changes in the county structure and missing data, the panel is unbalanced and the total number of usable observations is therefore 346. The data concerning patronage, vehicle-kilometres, costs and fares are supplied by The Swedish Public Transport Association (Svenska lokaltrafikföreningen, SLTF) to which local public transport authorities report several key statistics. Before 1986 the data was not reported in the same way and it is not possible to convert the series to be compatible and after 2001 local and regional travel is no longer reported separately. The rest of the data needed were obtained from Statistics Sweden (SCB).
Between 1986 and 2001 the total number of local trips by public transport in Sweden increased by 18,5 %, a figure sometimes used in order to portray public transport as a success story. However, this is misleading for two reasons. The uncharacteristic development of the county of Stockholm (including the Swedish capital) obscures the fact that patronage fell in most other counties. If Stockholm is excluded the total number of trips actually fell by 27,5 %. Looking at the development of per capita figures, the total number of trips per capita fell by 5,2 % during the period in question, and excluding Stockholm by 31 %.
Behind these aggregates, the demand differs immensely between counties. 634 million trips were made in Stockholm the year 2001, while only 280 thousand trips were made in the county of Gotland. Table 1 shows the heterogeneity of demand in terms of average per capita figures as well as the percentage change in number of trips per capita during the period in question.
The unique position of Stockholm is further underlined by these figures, not only is the number of trips per capita by far the highest but there has also been an increase in demand during the observed period. The only other counties where this has occurred in is Blekinge, Västernorrland and Skåne (1999–2001). In all other counties number of trips per capita has fallen since 1986.
Hardly surprising there is also a great deal of variation in service levels. Table 2 shows these variations in terms of average number of vehicle-kilometres per km2 as well as the percentage change during the observed period.
Again Stockholm stands out, this time as the region having the highest level of service in the public transport system. In most counties all public transport trips are made by bus but it should be pointed out that in the case of Stockholm the figures also include the underground system and the figures from Göteborg/Bohus and Östergötland include tram systems.Footnote 1
Measured in terms of revenue per trip,Footnote 2 the fare facing the traveller ranged from 1,96 SEK in the county of Västernorrland to 20,55 SEK in Kalmar making the monetary part of the generalised cost facing the consumer vary a great deal (Monetary terms are expressed in the 2001 price level). With an increase in real fares of 200 % during the period, the county of Kalmar also exhibits one of the most striking developments in this area, surpassed only by Jämtland where fares were increased by 251 %. At the other end of the scale, Blekinge and Västernorrland lowered their fares substantially (66 % and 73 % respectively). It is interesting to note that these two counties also are among the few where patronage increased. County averages and changes are shown in Table 3.
When it comes to income and car ownership the variation between counties is less than in the other variables. Gotland, together with Dalarna, Norrbotten and Värmland all exhibits car ownership levels exceeding 0,5 cars per capita (0,53, 0,52, 0,5 and 0,5 respectively) in 2001, while Stockholm was the only county with car ownership below 0,4 (0,39) cars per person. Average car ownership levels as well as income is shown in Table 4.
The variation in income is also relatively small between most counties although average income in Stockholm exceeded average income in Gotland by 40 % in 2001. During the period 1986 to 2001 the increase in average real income (in the 2001 price level) varied between 20 % (Västerbotten and Norrbotten) and 28 % (Stockholm).
3 Demand model and estimation
Demand for urban public transport is expressed as the number of trips per capita made in the urban areas (q) and the variables used to explain demand consists of fare (F), Vehicle-kilometres (V), Price of petrol (PP),Footnote 3 Income (Y) and Car ownership (C). The demand function is assumed to be logarithmic, therefore:

In which is assumed to be affected by the price of petrol and income so that:

Prices as well as income have been divided by a price index including all goods and services except public transport and petrol in order to preserve homogeneity. As previously mentioned, in three counties (Stockholm, Göteborg/Bohus and Östergötland) the number of trips made is an aggregate of bus trips and trips by underground (Stockholm) and tram (Göteborg/Bohus and Östergötland) which might be considered a problem. Vehicle-kilometres is also aggregated over different modes in those counties. Another potential problem that might occur when comparing the counties is that there might be differences in the preferences of people living in different areas, e.g. a difference between Stockholm and other areas. The latter is only a problem if these differences are not captured by the variation in the explanatory variables included in the model such as income and car ownership. These potential problems can be addressed in different ways. Some of the county differences is accounted for by including county specific effects (ϕ i ) in the model. These capture factors that differ between counties and are constant over time. ϕ i are also called unobserved effects in the literature, referring to the fact that they capture the effect of all (time invariant) factors that might affect q but not included in the other explanatory variables. In addition to county specific preferences this can also capture the effects of different demographic structure, geography, infrastructure etc. The most significant advantage of this is that it is possible to obtain correct estimates for the parameters of the variables actually included in the model even if they are correlated with an unobserved effect. This is not possible if the variable is simply left out of the model altogether [22]. The possibility of the unobserved effects being correlated with the explanatory variables in the model is also reason for not modelling the individual effects as part of the error term, i.e. using a random effects (RE) model. RE models are generally more suited to situations in which the individuals under study are drawn randomly from a larger population while the individuals in this case (the counties) constitute the entire population [22].
If all explanatory variables were strictly exogenousFootnote 4 this model could be estimated using the fixed effects estimator (FE) or the first difference estimator (FD). However, this is unlikely to be the case here. Vehicle-kilometres is most likely affected by the level of demand, either by past levels of demand if capacity adjustment takes time or by present levels if the adjustment is assumed to be instantaneous. In both cases vehicle-kilometres will be correlated with the error term ε thus violating the assumptions underlying both the FE and the FD estimator, rendering them both inconsistent. Wooldridge [22] suggests estimation in two steps where the first step is to remove the unobserved effects (ϕ i ) using either the FE or the FD transformation and the second step is to find variables to use as instruments for the endogenous variable in the transformed equation. After first differentiating, the demand equation is:

In this case lnF, lnPP, lnY and lnC might be used as instruments for ∆lnV (since they are assumed to be exogenous). However, using only these variables as instruments is likely to provide poor IV estimates due to limited correlation with V. Therefore additional variables that can work as instruments would be useful. Such variable has to be correlated with vehicle-kilometres but uncorrelated with the error term.
In this case the number of urban areas in each county, cost per vehicle-kilometre and size of the urban areas are used as additional instrument variables since they have been found to be correlated with vehicle-kilometres in previous studies (i.e. [15]).
In addition to allowing for county specific (time invariant) effects some other measures were takin in order to account for additional heterogeneity in the data. The models were also estimated using data where Stockholm and Göteborg/Bohus were excluded and also where Stockholm, Göteborg/Bohus, Malmöhus and Skåne were excluded. The same variables were statistically significant in those estimations and the differences in the estimated parameters in those models were very small. This indicates that the variation in travel behaviour between the counties with large cities and the rest can be explained reasonably well by the differences in the variables included in the model. In addition to this a model in which the effect of price changes were allowed to differ between counties were also tested using an interaction term (d i ·ΔF i,t , where d i is a county dummy) but the interaction terms were not found to be statistically significant as a group and therefore excluded from the model.
Results from estimation of (2) using the aforementioned variables as instruments for ∆lnV are shown in Table 5.
The Durbin-Watson value is 2,14 indicating that the model does not suffer from autocorrelation nor misspecification. A Breusch-Godfrey testFootnote 5 was also applied in order to test for higher order autocorrelation [23]. The null hypothesis of no autocorrelation could not be rejected on a 5 % level, indicating that the model does not suffer from autocorrelation of higher order. The model was also tested for heteroscedasticity using White’s general test.Footnote 6 The null hypothesis of no could not be rejected indicating that the model does not suffer from heteroscedasticity.
The coefficients for all variables except price of petrol are significant at the 5 % level or better and have the expected sign. The coefficients can be interpreted as (constant) elasticities. The results are in the range of what might be expected from comparison with previous results [5].
4 The effect of income changes
Returning to the question of how public transport demand is affected by increases (decreases) in income it is reasonable to assume that there is a direct effect on demand and an indirect effect working through the effects of income on car ownership. A change in income is likely to affect our travel behaviour in several ways. Higher income is generally associated with increased mobility in general and it is therefore likely that the overall number of trips made by all modes of transportation would increase as a response to such change. However, it is likely that higher income increase the possibility of owning a car and people having access to a car might be assumed to make fewer trips by public transport. The total effect on demand for public transport (QFootnote 7) from a change in income is:

Were

Therefore


Multiplying through with  give:
give:

Multiplying both nominator and denominator of the second term by C give

The first term in (3) ought to be positive, since higher income increase demand for travel in general, while the second term is negative (eQC is negative and eCY is positive).
In order to obtain ecy a dynamic model explaining car ownership by income and price of petrolFootnote 8 is estimated using the same data as when estimating the demand function. The model is:

The model (4) is subjected to the same tests for autocorrelation and heteroscedasticity as model (2) above, none of which indicated the presence of any problem with the model. The results are shown in Table 6
The long run elasticity of car ownership with respect to income is therefore found to be 0,21.Footnote 9 Using this result in combination with the results from the demand equation give:

Based on these results the total effect of income changes therefore seem to be close to zero. The confusion regarding the effects of income might very well be due to the omission of car ownership in the demand model in which case the resulting estimate is a mixture of both effects.
5 Conclusions
The focus of this article has been on the demand for local public transport. Using a constant elasticity demand equation it is found that the elasticities with respect to fare, vehicle-kilometres, income and car ownership are −0,4, 0,55, 0,34, and −1,37 respectively.
Changes in income affect public transport demand both directly and indirectly through increased car ownership. The direct effect is positive while the indirect effect is negative. Using the results presented in this article regarding the effects of income on car ownership and public transport demand, it is found that the total effect (in elasticity terms) of income is 0,05. Therefore it is concluded that the total effect of income on public transport demand is virtually zero.
This result is of importance for planning and future policy for public transport. If demand for public transport would have been falling with increased real income (as suggested by some previous studies, Dargay et al. 2003, 2002, Dargay and hanly 2002, Frankena 1978), public transport planners would have to expect decreasing demand for public transport when the general level of income is increased. This would make it increasingly harder for them to sustain a good level of service for the remaining passengers.
However, this study shows that the increase in demand from the increase in movement offsets the decrease caused by the increase in car ownership making the outlook for the future of public transport less bleak. If the total effect of increased income on public transport demand would have been negative, the possibility of using public transport as an instrument for alleviating environmental impacts from the transport sector, by gaining passengers from the private car, would have been small. Although the results are based on Swedish data, the methodology in finding the relevant effects is applicable to other areas as well. The actual figures might vary but it is not unlikely that similar results could be found in areas and countries with similar economic and social structure.
Notes
This also applies to the demand figures presented in Table 1.
Revenue per trip is obviously a simplification of the actual fare structure but it is likely to be a better measure of the (monetary) cost of a trip than the single trip fare due to many people using travel cards of different kinds.
The price of petrol is a yearly average calculated by the Swedish Petroleum and Biofuels Institute (SPBI), an association of propellant fuel and lubricant companies in Sweden. This is also a simplification since the price might vary between counties (although not by much due to competition) and over a year.
In a panel data model where yi,t are to be explained by a vector of variables xi,t, strict exogeneity applies when:
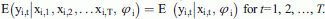 for t = 1, 2, …, T.
for t = 1, 2, …, T.In the test, the residuals from estimation of model 2
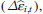 are regressed on the explanatory variables included in the model (2) and lagged residuals. It is then tested if the coefficients connected to the lagged residuals are (jointly) different from zero. If so, H0 of no autocorrelation is rejected.
are regressed on the explanatory variables included in the model (2) and lagged residuals. It is then tested if the coefficients connected to the lagged residuals are (jointly) different from zero. If so, H0 of no autocorrelation is rejected.The test regresses the squared residuals from estimation of model 2 (i.e.
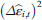 on the explanatory variables included in model(2), the explanatory variables from model (2) squared and interaction terms of the explanatory variables from model (2). The variables are then tested (jointly) for significance and if they not found significant H0 of no heteroscedasticity is rejected. In the present application, dummy variables for the counties were also included in the test in order to test for group wise differences in error variance. No indication of group wise differences were detected.
on the explanatory variables included in model(2), the explanatory variables from model (2) squared and interaction terms of the explanatory variables from model (2). The variables are then tested (jointly) for significance and if they not found significant H0 of no heteroscedasticity is rejected. In the present application, dummy variables for the counties were also included in the test in order to test for group wise differences in error variance. No indication of group wise differences were detected.Q refers to a general measure of demand, in the empirical study in question the number of trips per capita (q) is used as a measure of demand.
Vehicle-kilometers and public transport fare were also included in a previous version of the model, none of which were found significant and the former also had the wrong sign. They were therefore excluded.

References
International collaborative group on factors affecting public transport patronage (1980) The demand for public transport: report of the international collaborative study of the factors affecting public transport patronage. Transport and road research laboratory, Crowthorne
Goodwin PB (1992) A review of new demand elasticities with special reference to short and long run effects of price changes. J Transp Econ Policy 26:155–169
Oum TH, Waters WG, Yong JS (1992) Concepts of price elasticities of transport demand and recent empirical estimates. J Transp Econ Policy 26:139–154
Balcombe R, Mackett R, Paulley N, Preston J, Shires J, Titheridge H, Wardman M, White P (2004) The demand for public transport: a practical guide. (Transportation Research Laboratory Report TRL593). Transportation Research Laboratory, London, UK
Holmgren J (2007) Meta-analysis of public transport demand. Transp Res A Policy Pract 41:1021–1035
Nijkamp P, Pepping G (1998) Meta-analysis for explaining the variance in public transport demand elasticities in Europe. J Transp Stat 1:1–14
Kremers H, Nijkamp P, Rietveld P (2002) A meta-analysis of price elasticities of transport demand in a general equilibrium framework. Econ Model 19:463–485
Hensher DA (2008) Assessing systematic sources of variation in public transport elasticities: some comparative warnings. Transp Res A Policy Pract 42:1031–1042
Mohring H (1972) Optimization and scale economies in urban bus transportation. Am Econ Rev 62:591–604
Mohring H (1976) Transportation economics. Ballinger Press, Cambridge
Turvey R, Mohring H (1975) Optimal bus fares. J Transp Econ Policy 9:280–286
Jansson JO (1979) Marginal cost pricing of scheduled transport services. A development and generalisation of Turvey and Mohring’s theory of optimal bus fares. J Transp Econ Policy 13:268–294
Jansson JO (1984) Transport system optimization and pricing. Wiley, Chichester
Jara-Diaz SR, Gschwender A (2003) Towards a general microeconomic model for the operation of public transport. Transp Rev 23:453–469
Nelson GR (1972) An econometric model of urban bus transit operations. PhD-thesis, Rice University, Huston
Veatch JF (1973) Cost and demand for urban bus transit. PhD-thesis, University of Illinois, Chicago
Garbade KD, Soss NM (1976) Fare policies for mass transit deficit control: analysis by optimization. Transp Res 10:237–247
Frankena MW (1978) The demand for urban bus transit in Canada. J Transp Econ Policy 12:280–303
Wang GHK, Skinner D (1984) The impact of fare and gasoline price changes on monthly transit ridership: empirical evidence from seven U.S. transit authorities. Transp Res B Methodol 18:29–41
FitzRoy F, Smith I (1999) Season tickets and the demand for public transport. Kyklos 52:219–238
Holmgren J (2005) Demand and supply of public transport—the problem of cause and effect. In: International Conference on Competition and Ownership in Land Passenger Transport (2005). Competition and ownership in land passenger transport: selected refereed papers from the 8th International Conference (Thredbo 8), Rio de Janeiro, September 2003. Elsevier, Amsterdam
Wooldridge JM (2002) Econometric analysis of cross section and panel data. MIT Press, Cambridge and London
Greene WH (2003) Econometric analysis, 5 ed. Prentice-Hall, Upper Saddle River, NJ
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution License which permits any use, distribution, and reproduction in any medium, provided the original author(s) and the source are credited.
About this article
Cite this article
Holmgren, J. An analysis of the determinants of local public transport demand focusing the effects of income changes. Eur. Transp. Res. Rev. 5, 101–107 (2013). https://doi.org/10.1007/s12544-013-0094-0
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s12544-013-0094-0
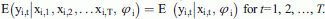 for t = 1, 2, …, T.
for t = 1, 2, …, T.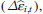 are regressed on the explanatory variables included in the model (2) and lagged residuals. It is then tested if the coefficients connected to the lagged residuals are (jointly) different from zero. If so, H0 of no autocorrelation is rejected.
are regressed on the explanatory variables included in the model (2) and lagged residuals. It is then tested if the coefficients connected to the lagged residuals are (jointly) different from zero. If so, H0 of no autocorrelation is rejected.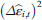 on the explanatory variables included in model(2), the explanatory variables from model (2) squared and interaction terms of the explanatory variables from model (2). The variables are then tested (jointly) for significance and if they not found significant H0 of no heteroscedasticity is rejected. In the present application, dummy variables for the counties were also included in the test in order to test for group wise differences in error variance. No indication of group wise differences were detected.
on the explanatory variables included in model(2), the explanatory variables from model (2) squared and interaction terms of the explanatory variables from model (2). The variables are then tested (jointly) for significance and if they not found significant H0 of no heteroscedasticity is rejected. In the present application, dummy variables for the counties were also included in the test in order to test for group wise differences in error variance. No indication of group wise differences were detected.