- Original Paper
- Open access
- Published:
A decision support framework for intermodal transport policy
European Transport Research Review volume 3, pages 167–178 (2011)
Abstract
Purpose
In recent years intermodal transport has received an increased attention due to problems of road congestion, environmental concerns and traffic safety. A growing recognition of the external effects of transport urges to go towards more sustainable transport modes. As a consequence, research and policy interest in intermodal freight transportation problems is growing.
Methods
In this paper the strengths of Operations Research (OR) modelling techniques applicable to decisions related to intermodal transport are used to develop a particular framework that is able to assess the performance of current and potential policy measures which affects the intermodal transport industry. The assessment framework includes three core models necessary to evaluate all relevant transport modes and aggregation levels.
Results
In the last section of the paper, the assessment framework is applied to a case study related to the location of a new intermodal barge terminal for which the optimal location is searched, the market area is analysed and the impact on the performance of the network is discussed.
1 Introduction
In recent years intermodal transport has received an increased attention due to problems of road congestion, environmental concerns and traffic safety. A growing recognition of the strategic importance of speed and agility in the supply chain is forcing firms to reconsider traditional logistic services. As a consequence, research and policy interest in intermodal freight transportation problems is growing. Macharis and Bontekoning [18] define intermodal transport as the combination of at least two modes of transport in a single transport chain, without a change of container for the goods, with most of the route travelled by rail, inland waterway or ocean-going vessel and with the shortest possible initial and final journeys by road. Intermodal transport may include various types of transport modes. In this paper we concentrate on the combination rail/road and waterways/road using containers as loading units.
The intermodal transport industry is characterized by multiple decision makers who need to work in collaboration in order for the transport system to run smoothly. An overview of the state-of-the-art research on planning problems in intermodal freight transport is presented by Caris et al. [1]. Intermodal transport, is a combination of different transport modes that has unique characteristics that distinguish it from other transport modes. Intermodal transport arises as a new transport mode when the chain is fully integrated and can be seen as a complete door-to-door service. An increased level of coordination is necessary to organize the intermodal transport flow. Decision-making support tools may assist the actors and stakeholders involved in intermodal operations.
Litman [17] and Rassafi and Vaziri [26] examine key sustainable transport goals, objectives and performance indicators. Sustainability can be grouped under three major goals: economic, social and environmental. Many indicators can be derived from the objectives defined with these goals. The main aim is to achieve an integrated, comprehensive and inclusive planning to allocate transport funding on alternative transport modes in a most beneficial way. This is possible through good governance and planning. In this paper we focus on the economic and environmental aspects of transport policy making for intermodal transport.
As several transport modes are included in an intermodal transport chain, intermodal transport costs involve a variety of transport activities. Figure 1 represents the intermodal cost function. Taking a door-to-door intermodal transport chain, the function allows calculating total intermodal transport cost between an origin and a destination.
Intermodal cost function Pekin [24]
At the port intermodal barge transport has larger handling costs compared to unimodal road transport. This is due to the cranes that are being used for the transhipment of containers on barges. The main haulage is carried by barge. The advantage of intermodal transport lies in the smaller variable costs during main haulage, as a result of the scale economies that are obtained by the large capacities that can be used. Scale economies, gained by the main haulage leg of an intermodal transport chain, can further be increased by an introduction of larger vessels. As the variable costs of barge transport is cheaper compared to road-only transport, longer distance covered by the intermodal leg will make intermodal barge transport more efficient than road-only transport. At the end of the chain, this advantage is partly compensated by the extra handling cost that has to be paid for the terminal handling. Terminal operations necessary to tranship the goods from one mode to another imply a vertical leap in the cost curve. Reliable terminal operations will contribute to prevent costs that take place in transhipping a container from the main haulage to the drayage. In order to achieve reliable operations and optimise the terminal processes, ICT applications will be needed. Special attention for empty containers is also required. The post haulage in the intermodal transport chain is performed by road. The cost curve of intermodal freight transport thus runs parallel to unimodal road transport. Once the total intermodal cost is calculated, it is possible to make comparisons with road-only transport, opening the way to a series of possible scenarios that can be assessed using an appropriate set of tools.
The attention of policy makers for intermodal transport, is based next to the economic efficiency, on the willingness to lower the externalities of transport and by doing so to come to a more sustainable transport system. Externalities are changes in welfare caused by economic activities without these changes being reflected in market prices [29]. In the field of transport these externalities arise when transport consumers/producers impose additional costs on society without having to bear these costs themselves. External costs are externalities expressed in monetary terms.
In economic literature, the most important external costs of transport are [7]:
-
Accidents;
-
Noise;
-
Air pollution;
-
Climate change;
-
Congestion;
Calculation of the relevant external costs in this specific case is based on best practices in the field of external cost assessment currently available in scientific literature [19]. Although there is growing consensus on the main methodological issues, there remain many uncertainties when performing an external cost assessment in practice. Marginal external costs of transport activities depend strongly on parameters such as fuel type, location (urban, interurban, rural), driving conditions (peak, off-peak, night) and vehicle characteristics (EURO standards) [8]. This explains the variety in results sometimes observed when looking at different external transport cost studies. According to Mihic et al. [20], water transport enables to achieve modern high-capacity transport of freight without harming the environment too much, meaning that it does not create much pollution and it does not harm the view of the landscape.
Figure 2 summarizes the external costs from traffic noise, accidents, climate gas and air pollution for three freight container transport modes: road, rail and inland waterway [25]. This study was based on a comparative external cost calculation for container and bulk transport on thirteen specific European trajectories. On all selected routes, a clear advantage of inland shipping became obvious, even if a bonus was assigned to railways regarding noise pollution (at equal exposure, railway noise leads to a lower percentage of annoyed people than road traffic noise). For container transport, the average total external costs of inland shipping are 78% below those of road and 68% below those of railway transport. External congestion costs for road transport are not even taken into account here.
Intermodal transport, incorporating more environmental modes such as barge, rail and short sea shipping can thus be said to have lower external costs in most of the trajectories (see for an overview of studies [12]). Carbon dioxide emissions of road transport and intermodal container transport can be found in Liao et al. [14] and Liao et al. [15].
In this paper three core models are developed to create an overall assessment framework for intermodal transport policies: a multimodal freight model (NODUS), a discrete event simulation model of the inland waterway network and its terminals (SIMBA) and the LAMBIT model supporting location analyses for Belgian intermodal terminals. The combination of the three models creates a decision support system that allows simulating policy measures to support the intermodal transport industry and foreseeing possible problems in the freight infrastructure network. The effectiveness and sustainability of policy measures in terms of modal shift, external costs and capacity restrictions can be analysed. In the next section, the context of intermodal transport in Belgium will be briefly presented. This will be followed in Section 3 by an outline of the three core models of the decision support framework. A complete case study will finally illustrate the use of the tools to solve the particular problem of the optimal localisation of an additional intermodal terminal along the Belgian inland waterways network (Section 4).
2 Intermodal transport in a policy context
Intermodal transport is promoted through policies that are addressed at all political levels. The policy maker’s role in intermodal transport policies is to assure an environment for a smooth functioning market, maintain a complete and interoperable multimodal transport network and promote its optimised use to minimise environmental externalities. Intermodal transport policy in Europe is based on a co-modal approach, the efficient use of different modes on their own and in combination to achieve a high level of both mobility and of environmental protection.
Various transport policies aim to initiate a modal shift of freight from unimodal road transport to modes that are environmentally more efficient (See [24] for an overview of intermodal transport policies).
In 2007, the European Commission (EC) announced a European freight transport action plan. One of the concepts introduced is that of “green transport corridors”. Green transport corridors include shortsea shipping, rail, inland waterways and road transport combinations to enable environmentally friendly transport solutions for the European industry. The EC also proposes to revise the Directive on the charging of road transport for infrastructure use (Eurovignette).
Addressed to potential customers, who mainly use road only transport, the policy aims to create awareness of the capabilities and advantages of the intermodal transport industry. A lot of initiatives are taken at the European level, but this section will limit the topic to what is proposed in Belgium, as the case study in Section 4 is concerned with this particular country.
Belgium has an extensive transport network to distribute containers that are arriving to the ports of Antwerp and Zeebrugge. The country is composed of two regions, Flanders and Wallonia. In the last decade, the Flemish government introduced various subsidy schemes for container barge waterways transport. The Walloon government follows this trend as well.
Regarding intermodal rail transport, the Flemish aid (N 566/02) for combined transport provided an annual budget of € 3 million for the acquisition of combined transport equipment, transshipment equipment and aid for information systems. The subsidy scheme, which expired end of 2003, covered investment costs of the railway operators with the objective to offer new combined transport operations, i.e. a new route, new types of traffic or a new contract, to expand existing combined transport operations or to maintain the capacity of existing combined transport operations. A new subsidy (N 249/04) is specifically designed to national intermodal rail transport. The Belgian government grants an annual budget of € 30 million to the intermodal operators, which offer transport services within Belgium of minimum 51 km. The subsidy is composed of a fixed part (20 Euros) and a variable part (maximum 0.40 Euros per kilometre). The objective of the aid scheme, which is extended till end 2008 (N 656/07), is to help maintain existing rail traffic levels of 300,000 ITU and to increase rail traffic by 20% over a period of 3 years.
In order to promote inland navigation, the Flemish government developed a policy measure that stimulates the construction of new quay walls coupled with a reduction of canal-dues. The public private partnership programme allows the co-financing of the construction of quay walls for 80% by the Flemish government and 20% by the private sector. The quays stay property of the Flemish government and the private investor guarantees that a fixed tonnage of freight will be transported by inland waterways in the 10 years to come. The programme, which established the support of the European Commission until 2010 (N 550/01 and N 344/04), realized a 66.5% growth in the inland waterways transport over the previous 5 years. In May 2007, the European Commission authorized another Flemish measure to grant a subsidy of 20 Euros per container transshipped at a Flemish inland container terminal from or to an inland waterway vessel (N 682/06).
Similar initiatives are developed in Wallonia. In March 2005, the European Commission authorized a Walloon measure to grant a subsidy scheme to promote intermodal barge transport in the Walloon region (N 247/04 and N 4/04). According to the government decision of December 2004, the Walloon government, with the objective of developing regular container services in Wallonia, started to subsidize investments at terminals, for example for transshipment infrastructure. The government decision also aims to modernize the fleet. In addition to the investment aid, a subsidy of 12 Euros is foreseen for containers that are transshipped at a Walloon inland container terminal from or to an inland waterway vessel (OPVN, 2006). Finally, a subsidy of 12 Euros is also applied for the terminal in Brussels (N 720/06).
3 Decision support framework for intermodal transport
3.1 General framework
Intermodal transport solutions are becoming increasingly important in Belgium. The growing attention on the intermodal transport sector from federal and regional governments is supported by academics. Within the DSSITP (Decision Support System for Intermodal Transport Policy) project, an assessment framework has been developed using three different models that are capable of assessing policies intended to enhance the growth of intermodal inland waterway and rail transport. Both combinations have a particular market structure and operations, but it is important to analyse them together in order to take care of potential competition distortions. The assessment of transport policy measures has been performed on a European scale by Tsamboulas et al. [28]. The authors focus on the potential of policy measures to produce a modal shift in favour of intermodal transport. Tan et al. [27] discuss a simulation model for a state-wide intermodal freight transportation network, with the objective to demonstrate interactions between transport modes under various intermodal policy changes. A strategic decision support system to plan logistics and distribution activities of manufacturers has been constructed by Moynihan et al. [21]. The DSSITP framework assesses policy measures and planning decisions related to the intermodal transport sector, taking multiple indicators into account. The impact of policy measures are measured on all related transport modes and at multiple aggregation levels.
The DSSITP framework, composed by the three core models acts as a platform to evaluate intermodal transport policies. Interaction between each model enables to achieve an integrated approach in transport modelling. An exercise has been performed to document inputs and outputs of the models.
Three core models, LAMBIT, SIMBA and NODUS make up the decision support system for intermodal transport policy making. The individual models will be shortly presented in the following subsections. Figure 3 presents the general assessment framework, in which the three models are integrated. Due to the combination of the three models, the analysis of policy measures is performed on multiple levels of aggregation over multiple transport modes. Each model has its specific purpose and outputs. The multimodal freight model NODUS is situated on the highest level of aggregation and constitutes the first step in the analysis of a potential policy measure. The NODUS model provides traffic prognoses which serve as inputs for the LAMBIT model and SIMBA model. The various outputs of the assessment framework are also stated in the same figure. The NODUS model produces aggregated outputs (flows) of the various transport modes, such as their accessibility, environmental impact and share in the modal split. Total costs of an intermodal service are measured. In addition, a module was developed for NODUS in order to provide optimal locations of terminals. These optimal locations can be introduced in the LAMBIT and SIMBA models. The LAMBIT model is scaled on the Belgian intermodal network. The model analyses the potential market area of a new terminal and assesses the impacts on existing terminals. It further produces cost comparison and potential modal shifts. The SIMBA model is situated on the lowest level of aggregation and produces detailed output related to the reliability, speed and capacity utilization of the waterway network. With the SIMBA model, the impact of volume increases in the network or the introduction of new intermodal barge terminals can be simulated. Also alternative consolidation strategies may be compared.
In order to demonstrate the capabilities of the general framework, first the individual transport models will be explained in the next subsections.
3.2 NODUS
A geographical multimodal transport network is made of links like roads, railways or waterways, on which vehicles moves; at its nodes, connecting infrastructures like terminals or logistics platforms where goods are loaded, unloaded, transhipped or processed in different ways can sometimes be found. To analyse transport operations over the network, costs or weights must be attached to these geographical links over which goods are transported and to the connecting points where goods are handled. However, most of these infrastructures can be used in different ways and with different costs. For example, ships of different sizes and operating costs can use the same waterway; at a terminal a truck's load can be transshipped on a train, bundled with some others on a ship or simply unloaded as it reached its destination. Normally, the costs of these alternative operations should be different, and a simple geographic network does not provide an adequate basis for detailed analyses of transports operations where the same infrastructure is used in different ways. To solve this problem, the basic idea is to create a virtual link with a specific cost for a particular use of an infrastructure [4, 6].
NODUS is a Geographic Information System (GIS) based software that proposes a methodology and an algorithm which creates in a systematic and quasi-automatic way a complete “virtual network” with all the virtual links corresponding to the different operations which are feasible on every real link or node of a geographic network [9, 11]. This permits to apply the methodology to extensive multimodal networks. In this way, a network with multiple modes and means can be represented by a unique but more complex network on which each link corresponds to a unique operation with a specific cost (see also [16]). Applying a shortest path algorithm on such a network provides a “route” that corresponds to the chain of operations from the loading point to the final destination. This route can very well correspond to an intermodal shipment. Nodus is also able to find out a set of alternative paths between each origin and destination, making it possible to spread the demand over several modes. A more in-depth discussion of this methodology can be found in [10].
Once a complete origin–destination demand matrix has been assigned on the network and calibrated, the amount of tons-km carried out by each transportation modes is used to compute the total emissions. Comparing these emissions for two scenarios (without and with an additional terminal) make it possible to evaluate the environmental impact.
3.3 LAMBIT
The Location Analysis Model for Belgian Intermodal Terminals (LAMBIT) is based on three main inputs: transportation networks (GIS), transport prices and container flows from the municipalities to and from the port of Antwerp. The GIS network has two main tasks. First of all, it visualises the real transportation network including the terminals. The second and vital characteristic of the network is its capability in serving as a database to include transport prices.
The transport prices are calculated based on the real market price structures for each transport mode and they are associated with the network layers. The variable costs are applied to the network layers and the fixed costs are attached to the nodes, which also indicate the origin and destination for each path.
The total price of intermodal transport is composed of the transshipment cost in the port of Antwerp to a barge or a wagon, the cost of the intermodal main haul (barge or rail), the transshipment cost in the inland terminal to a truck and the cost of final haulage by truck. The total intermodal transport cost is obtained by adding all of these fixed and variable costs.
Using a shortest path algorithm in ArcInfo, various simulations are conducted in order to find the shortest path and the attached transport costs from the port of Antwerp to each Belgian municipality via intermodal terminals and via road only. For each destination, the total transport costs for unimodal road, inland waterways/road and rail/road transport are compared and the cheapest option is selected. The market areas of each inland terminal are then highlighted on maps, which help to see how large the market area of each intermodal terminal is. The market area of a terminal is measured by the number of municipalities that are cheaper by intermodal transport. As a further step, the Belgian Institute for Statistics (ADSEI) data are used to show the amount of containers that are currently transported by road to the municipalities within the market area, which give an indication of the existing potential volume that can still be shifted from road transport to intermodal transport. This is particularly useful when a location of a new terminal needs to be analysed.
3.4 SIMBA
The discrete event Simulation model for InterModal BArge transport (SIMBA) covers the hinterland waterway network of the port of Antwerp, in order to analyze effects of future policy measures for intermodal barge transport or to analyze planning decisions of private stakeholders [2, 3]. The SIMBA and LAMBIT models are complementary to the NODUS model, which considers the whole set of origins and possible destinations on the observed network. SIMBA is also complementary to the LAMBIT model, as the latter proposes a macro-level approach.
Three interrelated components can be identified in the intermodal hinterland network. The first component in the intermodal freight transport network is the inland waterway network. From a simulation point of view, the inland waterway network is made up of terminals, waterway connections and container flows. Entities are defined as barges which originate from the different inland terminals and carry containers in round trips to the various ports. A second component is the port area of Antwerp. Barges may visit sea terminals on the left river bank and right river bank in the same round trip, go to Rotterdam or Amsterdam via the Scheldt-Rhine connection or sail to Zeebrugge via the Scheldt estuary. On the right and left river bank, barges queue for handling at the sea terminals. Barges moor as soon as enough quay length is available. The handling time at the sea terminal depends on the number of containers that need to be unloaded from or loaded into the inland vessel. In the inland waterway network as well as in the port area multiple locks are present. Therefore, lock planning constitutes a third major component. The operation of locks is one of the elements which most strongly affect waiting times of barges for lockage. A number of decision rules are defined to make the operations of the locks in the simulation model reasonably realistic.
To obtain the necessary input data, all intermodal terminals in the inland waterway network are asked for information to identify current container flows in the network. Real data on shuttle services is used as an input for the simulation model. For each shuttle service the following information is required: which type of barge is used, which destinations are visited and what is the average number of import and export containers for each destination. Container transport interacts with other freight flows. Therefore, the flow of non-containerized goods on the inland waterway network is introduced as an input in the simulation model. These flows affect the waiting times at locks. Information is also necessary on the network connections. The waterway administrators (Waterwegen en Zeekanaal nv, nv De Scheepvaart en Gemeentelijk Havenbedrijf Antwerpen) provided information on the number of locks on each waterway, distances between locks, average lockage times, number of lock chambers and size of the chambers. In the port area of Antwerp three clusters of locks connect the inner port area with the sea side. Data is required on the choice of locks when sailing in the port area. The average quay length available for handling inland navigation at sea terminals gives an indication of the service capacity in the port area of Antwerp. The port authority provided the average mooring time and time for loading and unloading in order to model service times of inland container barges in the port area. Service times in the port area include the time for mooring at each sea terminal plus the handling time of all import and export containers.
The SIMBA model produces detailed outputs related to the functioning of the waterway transport network. Real data on shuttle services is used as an input for the simulation model, constructed in the Arena simulation software. Arena is a simulation package based on queuing theory. It is designed for modeling discrete event simulations. For each shuttle service the following information is required in the simulation model: which type of barge is used, which destinations are visited and what is the average number of import and export containers for each destination. Container transport interacts with other freight flows. Therefore, the flow of non-containerized goods on the inland waterway network is introduced as an input in the simulation model. These flows affect the waiting times at locks. Information is also necessary on the network connections. The performance of the network elements with respect to reliability, speed and capacity utilization is measured. Table 1 gives an overview of performance measures which are generated by the simulation model. The turnaround time of shuttles is defined as the total time necessary for a barge to sail from an inland container terminal to the port area, visit all sea terminals and return to the inland terminal. The turnaround time depends on the waiting times at locks and in the port area. The outputs measured at locks are the percentage of barges that have to wait, the number of barges that have to queue and the waiting time of barges in the queue. In the port area the waiting time before handling is measured, as well as the number of vessels queueing for service. A final group of performance measures concerns the capacity utilization. In the port area this is expressed as the average percentage of quay length occupied. In the hinterland network the average and maximum number of barges on each network connection is recorded. Other performance measures can be added to the simulation model when necessary for future analyses.
4 An integrated case study
In the case study presented in this paper, the optimal location for an additional container terminal along the Belgian waterways is computed and its impact on the market area and network performances is assessed.
An additional module is developed in NODUS in order to implement an optimal location algorithm. The theoretical background involved will first be outlined. This will be followed by a brief description of the digitised network that was used. The obtained result (the new optimal location) and its potential impact on the modal shift are then discussed. Once the optimal location determined and the global impact of its implementation estimated, the second step of this case analyses the market area of the identified new terminal location. This result will be achieved using the LAMBIT model. Finally, the SIMBA model will be used during a third step in order to estimate the impact of the newly located terminal on the performances of the transport system.
4.1 Optimal location of a new terminal using NODUS
4.1.1 Optimal location of a new terminal
One of the possible policy measures to increase freight flows using intermodal transport is the opening of new container terminals on inland waterways or along rail connections. Such a terminal must be well located in order to reach this goal, which means that it will be chosen following a set of criteria as the geographic distribution of freight flows and their costs for transhipment. To achieve this work, an algorithm using these parameters has been implemented in NODUS. It locates new terminals taking the existing ones into account and considering the terminals as hubs. It is the p-Hub Median problem (p-HMP) first formulated by O’Kelly [22]. In the standard multiple-hub network problem (see [23]) for the different problem classes), three constraints are traditionally identified: it is assumed that all the hubs are connected directly to each other, that there is no direct connection between non-hub nodes, and that the non-hub nodes are each connected to a single hub. The inter-hub links consolidate the total flow coming from the origin hub (or any of its spoke nodes) to the destination hub (or any of its spoke nodes). The location of the hubs must be chosen from the set of nodes, N, considered as potential locations. Economies of scale can be associated with the transportation system between the hubs. The objective is to minimise the total transportation cost. Other problem formulations are available, but this one has been chosen because it enables to take explicitly into account the costs for pre- and post-haulage by road in addition to the cost of the main haul, which is an advantage when locating terminals in an intermodal context. The formulation used for the p-HMP is the one by Ernst and Krishnamoorthy [5] that considerably reduces the required computing time. The objective function of this problem tends to minimise the generalised cost (1) which comprises the costs for pre- and post-haulage by road plus the main haulage using the waterways (including possible economies of scale) and the transhipment at the terminals. The problem can be formulated as:
Inputs
- p :
-
number of terminals to locate
- h ij :
-
flow between origin i and destination j
- O i :
-
total flow from node i
- D i :
-
total flow to node i
- χ:
-
relative cost of pre-haulage
- α:
-
inter-hub discount (0 ≤ α ≤1)
- δ :
-
the relative cost of post-haulage
- C ik :
-
unit cost for route between node i and terminal located at node k
- C km :
-
unit cost for route between terminals located at nodes k and m
- T :
-
transhipment cost at terminal
Decision variables
-
X ik = 1 if node i is assigned to the terminal located at node k

-
0 otherwise
-
Yi km ≥ 0 is the traffic from node i that passes by terminals located at nodes k and m
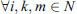
Minimise

Constraints






The algorithm finds p optimal locations in a set of determined potential locations on the network (1.1). Another constraint is that each centroid (aggregated origin or destination point of the freight) must be connected to a single terminal in order to reduce the size of the problem (1.2). In constraint (1.3), a centroid cannot be assigned to a terminal if the latter is not activated as so. Equation 1.4 is the divergence equation for commodity i at node k in a complete graph, where the demand and supply at the nodes is determined by the allocations X ik . The latter enables to keep the flows at the terminals. Constraints (1.5) and (1.6) are standard integrity constraints.
Each (i,j) pair in a p-HMP is analogous to a demand point in a p median problem (p-MP) in which the demand nodes are assigned to the nearest facilities. As it may not be ideal to assign the demand nodes to their nearest hub, the p-HMP relaxes this constraint.
In the application set up in the framework of the DSSITP project, 11 existing terminals were taken into account including those located into the ports of Antwerp and Zeebrugge. They were added to 50 other potential locations (N = 61) on the Belgian inland waterways and then the p-HMP was applied to this case in order to find one additional new optimally located terminal. These 50 potential new locations were selected homogeneously on the waterways network. Note that only network connections with a gauge at least equal to 1350 T are taken into account.
4.1.2 Network database
A network model able to assess the impact of the addition of a new terminal was developed. We used the origin–destination (OD) matrices for the year 2000, produced by NEA Transport Research and Training. The matrices give information about the type of commodity being transported, classified according to the Standard Goods Classification for Transport Statistics/Revised (NST/R chapters). Only the figures for NST/R Chapter 9, containing the demand for containers amongst other manufactured products, are taken into account in the model. The database contains region-to-region relations at the NUTS2 (Nomenclature of Territorial Units for Statistics) level, for the area of the EU25, plus Norway and Switzerland, and at the NUTS5 level for Belgium. The matrix provided by NEA is at the NUTS2 level. Therefore, in order to obtain figures at the communal (NUTS5) level for Belgium, an older matrix (1995) available at the NUTS5 level was used to disaggregate the matrix for 2000.
A digital representation of the networks for the different transportation modes (roads, railways and inland waterways) is also needed. The railway and road networks were taken from the Digital Chart of the World (DCW) and updated. The DCW is an Environmental Systems Research Institute, Inc. product originally developed for the US Defence Mapping Agency (DMA) using DMA data. The inland waterways network was digitised at the Group Transport & Mobility (GTM) research lab.
Finally, the borders of the NUTS 2 regions were provided by Geophysical Instrument Supply Co (GISCO) and a centroid for each region was located at the centre of the most urbanised area of the zone. These centroids are taken as the origins or destinations for the commodities. The same was done at the NUTS5 level for Belgium.
All these separate layers were finally connected together by the creation of “connectors” from each centroid to each modal layer. The complete set of layers can be considered as a geographical graph, comprising about 110,000 edges and 90,000 vertices.
A validation of the network model, comparing assigned flows and real counts along the networks was performed. The quality of the assignment can be considered as satisfactory, taking into account the fact that the demand data is nearby 10 years old. However, the methodology is robust and can be applied easily to newer data, if it were available.
5 Results
An optimal location was found at Roucourt on the Nimy-Blaton-Péronnes canal. Note that a new terminal is currently planned in this region, in Vaux. An analysis of the changes induced by the opening of such a terminal was further performed. It is indeed possible to estimate the impact on the modal split, on the total generalised transportation cost on the network and on the amount of containers handled at the existing terminals when Roucourt is introduced in the NODUS network model.
The modal share for intermodal transport (Table 2) increases by 2.87% in tons while road-only transport decreases by 0.07%. Expressed in tons.km, the modal share increases by 0.78% for waterways, and decreases by 0.02% for road. The total generalised cost on the network decreases by 0.05% with the additional terminal. The amount of containers handled at the terminals increases for all the existing terminals except for Avelgem from which Roucourt seems to catch some market area. This is probably due to their relative close locations on the network. Indeed, Roucourt can serve an area in Hainaut that is normally assigned to Avelgem. The total increase can be explained by the fact that the new terminal covers a new area currently not yet exploited by the existing terminals. This new terminal influences the distribution of freight flows in favour of intermodal transport. Even if the relative difference seems to be weak, it represents several millions of tons transferred from road to waterways, which can be considered as a good evolution towards a sustainable transport system.
5.1 Market area and potential of the new terminal using LAMBIT
With the LAMBIT model the market area and potential volume of the new intermodal terminal in Roucourt can now be analysed. The optimal location, which NODUS provided, is included as an additional inland waterways terminal in the LAMBIT model. Figure 4 visualises a small market area for the new terminal, based on the current market prices.
A terminal in Roucourt, takes 3 municipalities that are currently served by unimodal road transport. The new terminal in Roucourt is 28 km away from the terminal in Avelgem. The location of new terminal points at a possible common market area problem. Although the terminal in Roucourt is located in proximity with the terminal in Avelgem, it attracts municipalities that are outside the market area of Avelgem. This situation complements the outcome of NODUS, which showed that the new terminal influences the distribution of freight flows in favour of intermodal transport.
5.2 Impact on waterways network performance using SIMBA
In this subsection, the SIMBA model is applied to analyse the impact of the new intermodal barge terminal in Roucourt on the waterways network. The impact on network characteristics such as average and maximum waiting times at locks and in the port area can be measured. Potential bottlenecks and necessary capacity investments may also be deducted. The location and volume of a new intermodal barge terminal result from the NODUS and LAMBIT models. The container volume of the new terminal location is derived from the proportional market area of the new location compared with the current market area of existing terminals. The results of NODUS show that the terminal of Roucourt will have more or less the same size as the terminal in Gent and one third of the volume of Avelgem. A potential volume of 7,000 containers per year with the port of Antwerp as origin or destination is assumed. Vessels will sail via the Upper Scheldt to the port area in Antwerp. The Nimy-Blaton-Péronnes canal is navigable for vessels up to 1350 tons. As the terminal currently does not exist, assumptions have to be made regarding the service schedule offered to customers. Vessels of size 32 TEU and 66 TEU sail in a roundtrip to the port area. Three departures are equally distributed in a weekly schedule. Vessels may visit both clusters of sea terminals on the right and left river bank in a single roundtrip. As the new terminal is situated in the southern part of Belgium, it takes almost a day to sail from the hinterland to the port of Antwerp. Barges depart in the morning of day one in Roucourt and arrive at sea terminals in the morning of day two. No changes are made to the schedules of the existing inland terminals. A separate random-number stream is dedicated to each source of randomness in the model in order to synchronise the current and new situation as much as possible.
Performance measures relevant for the comparison of the current and new situation can be calculated. The current and future situation are both simulated for a time period of 672 h or 28 days. Ten simulation runs, each taking up only a few minutes of computation time, are performed to make a statistical comparison between the current and new situation. Table 3 gives the average turnaround times of all inland terminals, expressed in hours in the current and future situation. Inland vessels may only sail to Antwerp (Antw) or they can make a combined trip to Antwerp and Rotterdam (Rdam) or Amsterdam (Adam). The standard deviation is mentioned between brackets next to the average turnaround time. From Table 3 may be concluded that the introduction of a new terminal has no influence on the turnaround times of existing terminals. Shuttle services offered by the terminal in Roucourt incur a turnaround time of 63.31 h.
Table 4 summarises performance measures in the port area. The average and maximum waiting time before handling, expressed in hours, are given for the sea terminals on the right and left river bank. Next, the average and maximum utilisation of the quays on the right and left river bank are measured.
Paired-t confidence intervals are constructed to compare the results [13]. Table 5 presents the 95% confidence intervals for which the difference between the introduction of a new terminal in Roucourt and the current situation is significant. The average handling time in both clusters of sea terminals on the left and right river bank increases slightly due to the introduction of a new terminal in the waterways network. An increase of 0.5% is only a minor effect. No large impact is to be expected in light of the small market area of the new inland terminal. However, the analysis clearly demonstrates the possibilities of the SIMBA model and the DSSITP framework. The framework is able to quantify ex-ante the impact of policy measures that stimulate the emergence of new intermodal terminals.
6 Conclusions
This paper proposes a decision support framework to analyze policies supporting the intermodal transport industry. The framework consists of three models: NODUS, LAMBIT and SIMBA. The combination of the models allows an analysis at multiple levels of aggregation and for multiple transport modes. The framework is applied in a case study to analyse in depth the location of intermodal terminals. The NODUS optimisation model shows that in the current terminal landscape a terminal location at Roucourt might be the most interesting choice. Verification of the potential market area by the LAMBIT model shows that the terminal will make new municipalities open for intermodal transport that are currently served by unimodal road transport. Although a small market area exists for the new terminal, it complements a market for intermodal transport together with the terminal in Avelgem. The SIMBA model shows that the introduction of a new terminal has no influence on the turnaround times of existing terminals. The average handling time at sea terminals in the port area increases only slightly due to the introduction of a new terminal in the waterways network. The case study demonstrates the possibilities of the framework for supporting the decision makers in intermodal freight transport sector. The methodology can also be applied to other policy measures such as subsidies, internalisation of external costs and intermodal network.
References
Caris A, Macharis C, Janssens GK (2008) Planning problems in intermodal freight transport: accomplishments and prospects. Transport Plann Tech 31(3):277–302
Caris A, Macharis C, Janssens GK (2011) Network analysis of container barge transport in the port of Antwerp by means of simulation. J Transport Geogr 19(1):125–133
Caris A, Janssens GK, Macharis C (2009) Modelling Complex Intermodal Freight Flows. In: Aziz-Alaoui MA, Bertelle C (eds) Understanding complex systems series: from system complexity to emergent properties. Springer, Berlin, pp 291–300
Crainic TG, Florian M, Guélat J, Spiess H (1990) Strategic planning of freight transportation: stan, an interactive graphic system. Transport Res Rec 1283:97–124
Ernst AT, Krishnamoorthy M (1996) Efficient algorithms for the uncapacitated single allocation p-hub median problem. Location Science 4(3):139–154
Harker PT (1987) Predicting intercity freight flows. VNU, Utrecht
INFRAS/IWW (2004) External costs of transport: update study. INFRAS/IWW, Zürich
Int Panis L, Mayeres I (2006) Externe kosten van personenvervoer. In: M. Despontin and C. Macharis (eds.), Mobiliteit en (groot)stedenbeleid. 27ste Vlaams Wetenschappelijk Economisch congres, 19 and 20 October 2006, Brussels, 417-446
Jourquin B, Beuthe M (1996) Transportation policy analysis with a geographic information system: the virtual network of freight transportation in Europe. Transport Res C 4(6):359–371
Jonkeren O, Jourquin B, Rietveld P (2009) Modal-split effects of climate change: the effect of low water levels on the competitive position of inland waterway transport in the river Rhine area, Transportation Research A, doi:10.1016/j.tra.2009.01.004, Available online 28 February 2009
Jourquin B (1995) Un outil d'analyse économique des transports de marchandises sur des réseaux multi-modaux et multi-produits: Le réseau virtuel, concepts, méthodes et applications. PhD thesis, Facultés Universitaires Catholiques de Mons
Kreutzberger E, Macharis C, Woxenius J (2006) Intermodal versus unimodal road freight transport—a review of comparisons of the external costs. In: Jourquin B, Rietveld P, Westin K (eds) Transportation economics—towards better performing transport networks. Routledge, New York
Law AM (2007) Simulation modeling & analysis: Fourth edition, McGraw Hill
Liao CH, Tseng P-H, Lu C-S (2009) Comparing carbon dioxide emissions of trucking and intermodal container transport in Taiwan. Transport Res D Transport Environ 14(7):493–496
Liao C-H, Tseng P-H, Cullinane K, Lu C-S (2010) The impact of an emerging port on the carbon dioxide emissions of inland container transport. Energ Pol 38(9):5251–5257
Limbourg S, Jourquin B (2009) Optimal rail-road container terminal locations on the European network. Transport Res E 45:551–563
Litman T (2011) Well measured. Developing indicators for comprehensive and sustainable transport planning. Victoria Transport Policy Institute
Macharis C, Bontekoning YM (2004) Opportunities for OR in intermodal freight transport research: a review. Eur J Oper Res 153:400–416
Maibach M, Schreyer C, Sutter D (INFRAS), Van Essen HP, Boon BH, Smokers R, Schroten A (CE Delft), Doll C (Fraunhofer Gesellschaft-ISI), Pawlowska B, Bak M (University of Gdansk) (2008) Handbook on estimation of external cost in the transport sector. Internalisation Measures and Policies for All external Cost of Transport (IMPACT), Version 1.1., European Commission DG TREN, Delft, CE, The Netherlands
Mihic S, Golusin M, Mihajlovic M (2011) Policy and promotion of sustainable inland waterway transport in Europe—Danube River. Renew Sustain Energy Rev 15(4):1801–1809
Moynihan GP, Raj PS, Sterling JU, Nichols WG (1995) Decision support system for strategic logistics planning. Comput Ind 26:75–84
O’Kelly M (1987) A quadratic integer program for the location of interaction hub facilities. Eur J Oper Res 32:393–404
O’Kelly M, Miller H (1994) The hub network design problem: a review and synthesis. J Transport Geogr 2(1):31–40
Pekin E (2010) Intermodal transport policy: a GIS-based intermodal transport policy evaluation model. PhD Thesis. Brussels. VUB
Planco Consulting GmbH (2007) Economical and ecological comparison of transport modes: road, railways, inland waterways. Summary of findings. Study prepared on behalf of the Federal German Water and Shipping Administration represented by the Water and Shipping Directorate East, November 2007, Essen, Germany, p 39
Rassafi AA, Vaziri M (2005) Sustainable transport indicators: definition and integration. Int J Environ Sci Tech 21:83–96
Tan A, Bowden R, Zhang Y (2004) Virtual simulation of statewide intermodal freight traffic. Transport Res Rec 1873:53–63
Tsamboulas D, Vrenken H, Lekka AM (2007) Assessment of transport policy potential for intermodal mode shift on a European scale. Transport Res A 41(8):715–733
Weinreich et al (1998) External quality valuation. contribution to the final report of the QUITS project, Mannheim
Acknowledgement
We thank the Belgian Science Policy (BELSPO) for their support on our research project DSSITP (Decision Support System for Intermodal Transport Policy) in the research programme "Science for a Sustainable Development—call 2", under contract number SD/TM/08A.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Macharis, C., Caris, A., Jourquin, B. et al. A decision support framework for intermodal transport policy. Eur. Transp. Res. Rev. 3, 167–178 (2011). https://doi.org/10.1007/s12544-011-0062-5
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s12544-011-0062-5